Lecture 05: Connections to non-Bayesian Analysis and Hierarchical Models

Chun-Hao Yang

Connections to non-Bayesian Analysis

\[ \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\R}{\mathbb{R}} \newcommand{\E}{\mathbb{E}} \renewcommand{\P}{\mathbb{P}} \newcommand{\var}{{\rm Var}} % Variance \newcommand{\mse}{{\rm MSE}} % MSE \newcommand{\bias}{{\rm Bias}} % MSE \newcommand{\cov}{{\rm Cov}} % Covariance \newcommand{\iid}{\stackrel{\rm iid}{\sim}} \newcommand{\ind}{\stackrel{\rm ind}{\sim}} \renewcommand{\choose}[2]{\binom{#1}{#2}} % Choose \newcommand{\chooses}[2]{{}_{#1}C_{#2}} % Small choose \newcommand{\cd}{\stackrel{d}{\rightarrow}} \newcommand{\cas}{\stackrel{a.s.}{\rightarrow}} \newcommand{\cp}{\stackrel{p}{\rightarrow}} \newcommand{\bin}{{\rm Bin}} \newcommand{\ber}{{\rm Ber}} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \]

Introduction

• In the previous lecture, we saw that MLE and MAP are related.
• We will discuss this relationship in more details and explore how this relationship benefits us.
• MLE and MAP are not the only connection between Bayesian and non-Bayesian analysis.
• We will discuss two other examples: bootstrap and random effect model.

MLE vs MAP

• Given \(X_1, \ldots, X_n \iid f(x\mid\theta)\), the likelihood function is

\[\ell(\theta\mid x_1,\ldots,x_n) = \prod_{i=1}^n f(x_i\mid\theta) = f(x_1,\ldots,x_n\mid\theta).\]

• Suppose we choose \(\pi(\theta) \propto 1\). The posterior is¹

\[ \pi(\theta \mid x_1, \ldots, x_n) \propto f(x_1,\ldots,x_n\mid\theta)\pi(\theta) = f(x_1,\ldots,x_n\mid\theta). \]

• Therefore

\[ \hat{\theta}_{\text{MAP}} = \argmax_{\theta}\pi(\theta \mid x_1, \ldots, x_n) = \argmax_{\theta}\ell(\theta\mid x_1,\ldots,x_n) = \hat{\theta}_{\text{MLE}}. \]

1. We need to make sure that the posterior is proper; otherwise, this equation is meaningless.

Asymptotics of MLE

• Let \(X_1, \ldots, X_n \iid f(x\mid \theta)\) and \(\hat{\theta}_n\) be the MLE of \(\theta\).
• Under some regularity conditions on \(f(x\mid\theta)\), the MLE is asymptotically normally distributed and efficient (having the smallest variance).
• That is, \[ \sqrt{n}\left(\hat{\theta}_n-\theta\right) \stackrel{d}{\rightarrow} N\left(0, I(\theta)^{-1}\right) \] where \(I(\theta)\) is the Fisher information of \(f(x\mid\theta)\).
• An important application of this result is the approximate confidence interval for \(\theta\) \[ \P\left(\hat{\theta}_n - z_{\alpha/2}[nI(\hat{\theta}_n)]^{-1/2} \leq \theta \leq \hat{\theta}_n + z_{\alpha/2}[nI(\hat{\theta}_n)]^{-1/2} \right) \approx \alpha. \]

Asymptotics of Bayesian inference

• The Bernstein-von Mises Theorem states that under some regularity conditions, the posterior distribution is asymptotically normal centered at the MLE.
• See Section 10.2 of Van der Vaart (2000) for rigorous arguments.
• The regularity conditions include:
  • the posterior must be proper, and
  • the prior is (strictly) positive in a neighborhood around the true parameter (this is a strong condition in high dimensions), etc.
• Roughly speaking, the Bernstein-von Mises theorem works well on a problem with few parameters and large dataset containing iid samples. For complicated problems like nonparametric problems, it might not work as well as you expect¹.

Van der Vaart, A. W. (2000). Asymptotic statistics.

1. See this blog post for an interesting discussion on Bernstein-von Mises Theoerm.

Normal approximation to the posterior

• If the posterior \(\pi(\theta\mid x)\) is unimodal and roughly symmetric, it can be convenient to approximate it by a normal distribution.
• That is, the logarithm of the posterior density is approximated by a quadratic function of \(\theta\).
• Consider Taylor series expansion of \(\log \pi(\theta\mid x)\) centered at the posterior mode (MAP) \(\hat{\theta}\) \[ \log \pi(\theta \mid x)=\log \pi(\hat{\theta} \mid x)+\frac{1}{2}(\theta-\hat{\theta})^T\left[\frac{d^2}{d \theta^2} \log \pi(\theta \mid x)\right]_{\theta=\hat{\theta}}(\theta-\hat{\theta})+\cdots \]
• That is, \[\begin{align*} \pi(\theta \mid x) \approx N\left(\hat{\theta},[I(\hat{\theta})]^{-1}\right) \end{align*}\] where \(I(\theta)\) is the observed information, \(I(\theta)=-\frac{d^2}{d \theta^2} \log \pi(\theta \mid x)\).

Normal approximation to the posterior

• If the approximation is good, we can construct an approximate credible interval without resorting to sampling techniques.
• In practice, however, it is almost impossible to check how good or bad the approximation is, especially when the parameter is high-dimensional.
• Even for low-dimensional parameter, if the posterior is multi-modal, the normal approximation will be terrible.
• In a later lecture, we will introduce a technique, called variational inference, which allows us to approximate the posterior using any parametric family, not just normal.

Bootstrap and Bayesian Inference¹

• Bootstrap is a method proposed by Efron (1979)² for deriving the sampling distribution of a statistic.
• It is based on resampling from the empirical distribution, which converges to the true population distribution (Glivenko-Cantelli theorem).
• Example: \(X_1, \ldots, X_n \iid F\) and \(\bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_i\).
• A bootstrap sample \(X_1^*, \ldots, X_n^*\) is obtained from \(X_1, \ldots, X_n\) using sampling with replacement.
• The sampling distribution of \(\bar{X}_n\) can be estimated/approximated by the distribution of \(\bar{X}^*_n = \frac{1}{n}\sum_{i=1}^n X_i^*\), which is called the bootstrap distribution.

1. Ch. 8.4 in Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction.

2. B. Efron. (1979) Bootstrap Methods: Another Look at the Jackknife. Annals of Statistics 7(1) 1 - 26.

Bootstrap and Bayesian Inference

• There are some similarities between bootstrap and Bayesian inference:
  1. They both treat the sample as fixed and given.
  2. Based on the sample, they both construct a distribution: bootstrap distribution vs posterior distribution.
• When will they be (approximately) the same?
• Suppose \(X_1, \ldots, X_n \mid p \iid \text{Ber}(p)\) and \(p \sim \text{Beta}(\alpha, \beta)\). Then \[ p \sim \text{Beta}\left(\alpha + \sum X_i, \beta + n - \sum X_i\right). \]
• Letting \(\alpha \to 0\) and \(\beta \to 0\), we have a noninformative prior and \[ p \mid X_1,\ldots, X_n \sim \text{Beta}\left(\sum X_i, n-\sum X_i\right). \]

Bootstrap and Bayesian Inference

• Consider a bootstrap sample \(X_1^*, \ldots, X_n^*\) (obtained from \(X_1,\ldots,X_n\) using sampling with replacement).
• Actually, \(X_1^*,\ldots, X_n^*\mid X_1,\ldots, X_n \iid \text{Ber}(\hat{p})\), where \(\hat{p} = \frac{1}{n}\sum X_i\).
• Let \(\hat{p}^* = \frac{1}{n}\sum X_i^*\). What is the bootstrap distribution \(\hat{p}^* \mid X_1,\ldots, X_n\)?
• Let’s do some experiment!

Bootstrap and Bayesian Inference

set.seed(124)
p <- 0.4; n <- 100; X <- rbinom(n, 1, p)
p_hat <- mean(X)

# bootstrap
B <- 10^3
p_boot <- rep(0, B)
for(i in 1:B){
    X_boot <- sample(X, size = n, replace = TRUE)
    p_boot[i] <- mean(X_boot)
}

hist(p_boot, freq = FALSE, main = "Bootstrap Distribution", xlab = "p")
curve(dbeta(x, n*p_hat, n*(1-p_hat)), add = T, col = "red")
abline(v = p, lty = 2, col = "green", lwd = 4)
abline(v = p_hat, lty = 2, col = "blue", lwd = 4)

Bootstrap and Bayesian Inference

The red curve is the posterior distribution; the blue dashed line is the MLE.

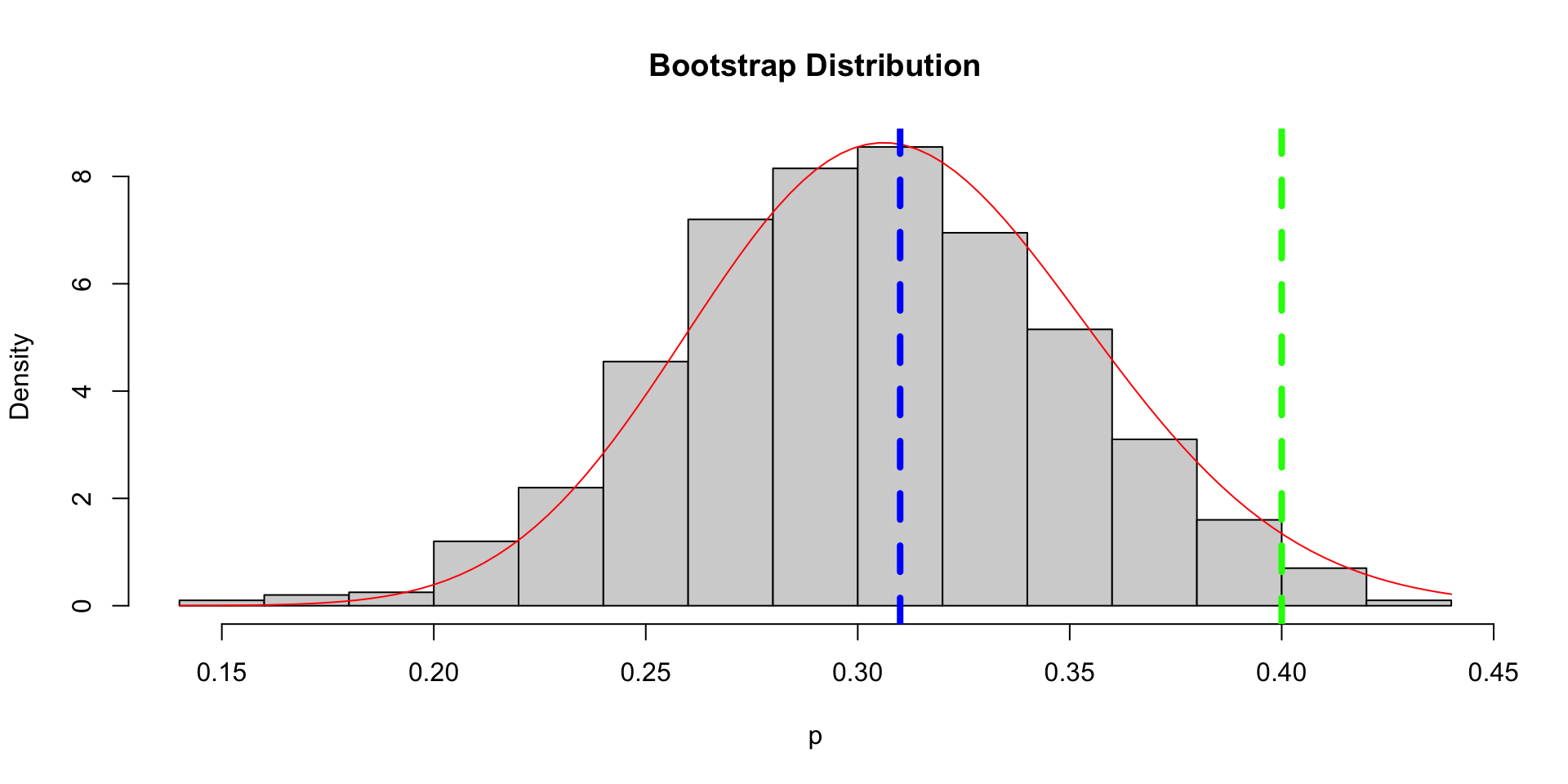
Bootstrap and Bayesian Inference

• In this sense, the bootstrap distribution represents an (approximate) nonparametric posterior distribution under a noninformative prior.
• But this bootstrap distribution is obtained painlessly – without having to formally specify a prior and without having to sample from the posterior distribution.
• Hence we might think of the bootstrap distribution as a “poor man’s” posterior.

Distributional estimates

• One of the advantages of Bayesian inference is that the entire inference is based the posterior distribution, rather than a single point estimate or an interval.
• The posterior distribution is just one example of distributional estimate, which use a distribution for inference.
• Bootstrap distribution is another example.
• There is a frequentist concept, called the confidence distribution, proposed by Neyman (1937)¹.
• The confidence distribution contains confidence interval of any level.
• Fraser (2011)² also discussed how the Bayesian posterior and the confidence distribution are related.

1. Neyman, J. (1937). Outline of a theory of statistical estimation based on the classical theory of probability. Phil. Trans. Roy. Soc

2. Fraser, D. A. S. (2011). Is Bayes Posterior just Quick and Dirty Confidence? Statistical Science, 26(3), 299–316.

Random effect models

• Fixed effect model: \(Y_i = \beta_0 + \beta X_i + \varepsilon_i\), \(\varepsilon_i \iid N(0, \sigma^2)\)
  • The parameter \(\beta\) is the fixed effect of the factors \(X\).
  • With a unit increase in \(X\), \(Y\) is expected to increase by \(\beta\).
  • Use (regularized) least squares to obtain an estimate for \(\beta\).
  • The effect is the same for each observation
• Random effect model: \(Y_i = \beta_0 + \gamma_iX_i + \varepsilon_i\), \(\gamma_i \sim N(\beta, \tau^2)\), \(\varepsilon_i \iid N(0, \sigma^2)\)
  • \(\gamma_i\) is the random effect in this model
  • The effect is different for each observation and, on average, \(Y\) is increase by \(\beta\) with a unit increase in \(X\).

Mixed effect model

• A model with both fixed effects and random effects is called a mixed effect model.
• This model is commonly used in biostatistics, psychology, economics, etc.
• A typical mixed effect model: \[ Y = X\beta + Z\gamma + \varepsilon, \quad \varepsilon \sim N(0, \sigma^2) \] where \(\beta\) is the unknown fixed effect and \(\gamma \sim N(\nu, \Psi)\) is the unknown random effect.

Sleep deprivation study

Data description

We use the sleepstudy dataset in the lme4 R package.

This dataset contains the average reaction time per day (in milliseconds) for subjects in a sleep deprivation study described in Belenky et al. (2003)¹, for the most sleep-deprived group (3 hours time-in-bed; 18 subjects) and for the first 10 days of the study. Days 0-1 were adaptation and training (T1/T2), and day 2 was baseline (B); sleep deprivation started after day 2.

1. Gregory Belenky, Nancy J. Wesensten, David R. Thorne, Maria L. Thomas, Helen C. Sing, Daniel P. Redmond, Michael B. Russo and Thomas J. Balkin (2003) Patterns of performance degradation and restoration during sleep restriction and subsequent recovery: a sleep dose-response study. Journal of Sleep Research 12, 1–12.

Data description

library(lme4)
library(tidyverse)
library(kableExtra)
data("sleepstudy")
sleepstudy |> head() |> kbl(format="markdown")

Reaction	Days	Subject
249.5600	0	308
258.7047	1	308
250.8006	2	308
321.4398	3	308
356.8519	4	308
414.6901	5	308

First attempt: simple linear regression

• Let \(Y\) be the reaction time and \(X\) be the Day variable.
• We want to see the negative impact of consecutive sleep loss in reaction time.
• A simple linear model: \(Y = \beta_0 + \beta_1 X\).

library(sjPlot)
sleepstudy |>
    lm(Reaction ~ Days, data = _, subset=Days>=2) |>
    tab_model()

	Reaction
Predictors	Estimates	CI	p
(Intercept)	245.10	223.31 – 266.88	<0.001
Days	11.44	7.78 – 15.09	<0.001
Observations	144
R2 / R2 adjusted	0.212 / 0.207

Individual difference

However, this model does not take into account the individual difference, i.e., the difference between subjects.

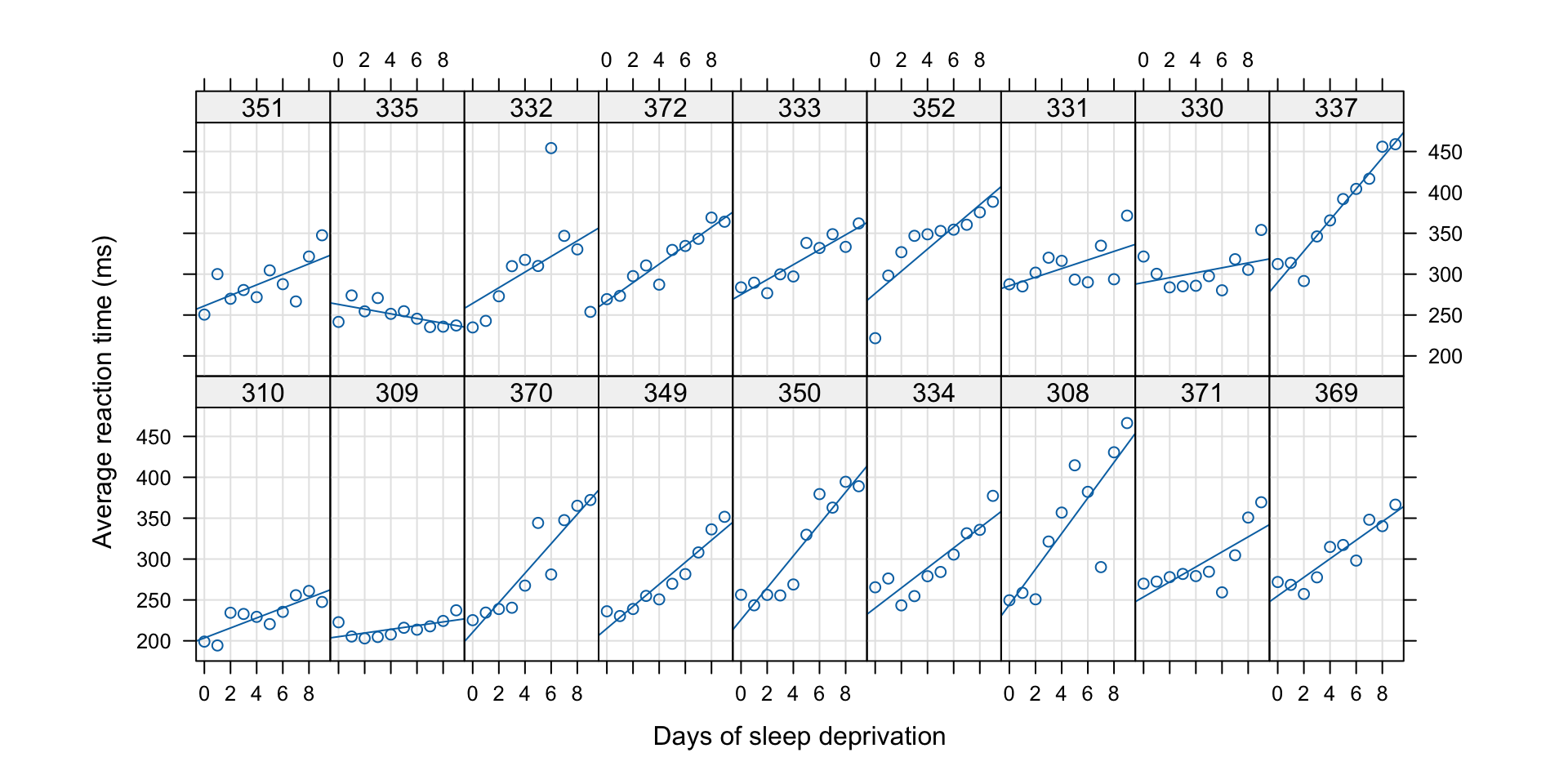
Second attempt: Mixed effect model

• We allow each subject to have its own intercept and effect: \[ Y_{ij} = b_{0,i} + b_{1,i} X_{j}, \quad i = 1,\ldots, 18, j = 0,\ldots, 9 \] where \(Y_{ij}\) is the reaction time of \(i\)th subject in Day \(j\).
• Note that we are not interested in the effects for each individuals.
• We just want to identify how much the individual difference contributes to the un-explained variation of the model.
• We assume that \(b_{0,i} \iid N(\beta_0, \tau_0^2)\) and \(b_{1,i} \iid N(\beta_1, \tau_1^2)\) are independent.
• The frequentist interpretation of this assumption is that the subjects are randomly selected, so there is randomness in the individual coefficients.
• The parameters \(\beta_0\) and \(\beta_1\) are unknown and fixed.

Second attempt: Mixed effect model

sleepstudy |>
    lmer(Reaction ~ Days + (1|Subject) + (0+Days|Subject), 
         data = _, subset=Days>=2) |>
    tab_model(show.icc = FALSE,show.obs = FALSE, show.ngroups = FALSE)

	Reaction
Predictors	Estimates	CI	p
(Intercept)	245.10	227.71 – 262.49	<0.001
Days	11.44	7.97 – 14.90	<0.001
Random Effects
σ2	662.92
τ00 Subject	831.93
τ11 Subject.Days	39.50
ρ01
ρ01
Marginal R2 / Conditional R2	0.316 / 0.697

Bayesian approach to mixed effect models

• The random effect assumption looks like a prior distribution on the coefficients.
• A mixed model \[ Y = X\beta + Z\gamma + \varepsilon, \quad\gamma \sim N(\nu, \Psi), \varepsilon \sim N(0, \sigma^2) \] can be rewritten as \[\begin{align*} Y \mid \gamma & \sim N(X\beta + Z\gamma, \sigma^2)\\ \gamma & \sim N(\nu, \Psi) \end{align*}\]
• A Bayesian approach puts priors on the parameters: \[\begin{align*} Y \mid \gamma, \beta, \sigma^2 & \sim N(X\beta + Z\gamma, \sigma^2)\\ \gamma \mid \nu, \Psi & \sim N(\nu, \Psi)\\ \beta, \nu, \sigma^2, \Psi & \sim \pi(\beta, \nu, \sigma^2, \Psi) \end{align*}\]

Bayesian approach to mixed effect models

Use stan_lmer to fit a Bayesian mixed effect model

library(rstanarm)
sleep_lmer_B <- stan_lmer(Reaction ~ Days + (1|Subject) + (0+Days|Subject), 
                          data = sleepstudy)

• Use summary(sleep_lmer_B) to check the fitted result
• Use prior_summary(sleep_lmer_B) to check the priors used in the model

Wrap-up

• Random effects are also called variance components, since we are more interested in the variance of the random effect rather than the effect itself.
• Mixed effect model is just one example of hierarchical models (or multi-level models).
• A hierarchical model contains many sub-models that are linked by some hierarchical relations.
• In the previous example, we can partition the dataset into smaller pieces by subject and hence subject is a hierarchy in this dataset.
• Note that a hierarchical model need not be a Bayesian model. However, Bayesian approach is a natural way to fit a hierarchical model.

Hierarchical Models

Motivation

• Some problems have intrinsic hierarchical structures, e.g., samples are grouped by some covariates (gender, ethnicity, etc.).
• In practice, simple nonhierarchical models are usually inappropriate for hierarchical data: with few parameters, they generally cannot fit large datasets accurately, whereas with many parameters, they tend to ‘overfit’.
• When parameters are only exchangeable rather than independent, a hyperprior is needed (de Finetti’s Theorem). That is, the subscripts of the parameters convey no information.

Meta-analysis

• Meta-analysis is an increasingly popular and important process of summarizing and integrating the findings of research studies in a particular area.

• The article “Why Science Is Not Necessarily Self-Correcting” by Ioannidis (2012) pointed out that sometimes fundamental fallacies remain unchallenged and are only perpetuated.

• You can find a detailed introduction to meat-analysis and different approaches to meta-analysis in https://bookdown.org/MathiasHarrer/Doing_Meta_Analysis_in_R/.

Ioannidis, J. P. (2012). Why science is not necessarily self-correcting. Perspectives on Psychological Science, 7(6), 645-654.

Clinical trials of beta-blockers

Data description

• Beta-blocker is a family of drugs that affect the central nervous system and can relax the heart muscles.
• This dataset summarizes mortality after myocardial infarction in 22 clinical trials.
• Each clinical trial consists of two groups of heart attack patients randomly allocated to receive or not receive beta-blockers.
• The dataset is available at http://www.stat.columbia.edu/~gelman/book/data/meta.asc.
• The aim of a meta-analysis is to provide a combined analysis of the studies that indicates the overall strength of the evidence for a beneficial effect of the treatment under study.

Data description

meta <- read.table("http://www.stat.columbia.edu/~gelman/book/data/meta.asc", 
                  header = TRUE, skip = 4)
meta |> head() |> kbl()

study	control.deaths	control.total	treated.deaths	treated.total
1	3	39	3	38
2	14	116	7	114
3	11	93	5	69
4	127	1520	102	1533
5	27	365	28	355
6	6	52	4	59

Odds ratio

• The odds ratio is the ratio of the odds death in the treatment group and the odds of death in the control group \[ \rho = \left. \frac{p_{\text{treat}}}{1-p_{\text{treat}}} \middle/ \frac{p_{\text{con}}}{1-p_{\text{con}}} \right. . \]
• We concentrate the inference on the log of the odds ratios \(\theta = \log \rho\) for each clinical trial.

Normal approximation to the likelihood

• Let \(y_{ij}\) and \(n_{ij}\) be the number of deaths and subjects of the \(i\)th group (\(1=\) treated, \(0 =\) control) in study \(j\).
• For each study \(j\), we estimate \(\theta_j\) by \[ \hat{\theta}_j=\log \left(\frac{y_{1 j}}{n_{1 j}-y_{1 j}}\right)-\log \left(\frac{y_{0 j}}{n_{0 j}-y_{0 j}}\right), \] with approximate sampling variance \[ \sigma_j^2=\frac{1}{y_{1 j}}+\frac{1}{n_{1 j}-y_{1 j}}+\frac{1}{y_{0 j}}+\frac{1}{n_{0 j}-y_{0 j}}. \]
• Thus \(\hat{\theta}_j \sim N(\theta_j, \sigma_j^2)\) approximately.

Odds ratio

meta_summary <- meta |>
    mutate(treated.odds = treated.deaths/(treated.total - treated.deaths),
           control.odds = control.deaths/(control.total - control.deaths),
           log.odds.ratio = log(treated.odds) - log(control.odds), 
           var = 1/treated.deaths + 1/(treated.total - treated.deaths) + 
               1/control.deaths + 1/(control.total - control.deaths)) |>
    select(c(study, log.odds.ratio, var)) 
meta_summary |> head() |> kbl(digits = 4)

study	log.odds.ratio	var
1	0.0282	0.7230
2	-0.7410	0.2334
3	-0.5406	0.3187
4	-0.2461	0.0191
5	0.0695	0.0788
6	-0.5842	0.4566

Goal of the inference

• Now we have the log odds ratios and their sampling variances from 22 studies.
• How are these studies related to each other?
  • Are they identical replications of each other, i.e., the studies are independent samples from a common population?
  • Are they completely unrelated?
• A more realistic assumption is that they are somewhere between the two extremes.
• Exchangeablity assumption: the parameters \(\theta_j\) are exchangeable.
  • We cannot distinguish \(\theta_j\)’s before we see that data.
  • Therefore \[ (\theta_1, \ldots, \theta_{22}) \sim \pi \Leftrightarrow \theta_i \iid \pi(\theta\mid\phi), \phi \sim \nu. \]

A hierarchical model

• Likelihood: \(\hat{\theta}_j \sim N(\theta_j, \sigma^2_j)\), \(j = 1,\ldots, 22\).
  • Assume the \(\sigma^2_j\)’s are known (given by the sampling variance computed before).
• Prior: we use the exchangeable normal prior for \(\theta_j\), \[ \theta_j \mid \mu, \tau \iid N(\mu, \tau^2) \] where \(\mu\) and \(\tau\) are unknown hyperparameters.
• Hyperprior: for \(\mu\) and \(\tau\) \[\begin{align*} \mu & \sim \pi(\mu) \propto 1\\ \tau & \sim \text{Unif}(0, A) \end{align*}\] for some large \(A\).
• Computation is left as homework.

Weakly informative priors for variance parameters

• For the variance parameter \(\tau\), we use the uniform prior \(\text{Unif}(0, A)\), which is a proper noninformative prior.
• Another choice is Inverse-Gamma\((\epsilon, \epsilon)\), with small \(\epsilon\).
• How about the Jeffreys prior?
  • To compute the Jeffreys prior, you need to first find the marginal distribution \(f(x\mid \mu, \tau) = \int f(x \mid \theta) \pi(\theta \mid \mu, \tau) d\theta\).
  • Then compute the Fisher information of \(f(x \mid \mu, \tau)\).
  • Both steps are difficult!!
• A bad news is that the posterior of \(\tau\) is sensitive to the choice of prior. You will see this in your homework.
• Read Section 5.7 of BDA for more details.