Lecture 07: Markov Chain Monte Carlo

Chun-Hao Yang

Motivation

  • Suppose now we have the posterior distribution \(\pi(\theta \mid x)\) for our problem.
  • We need to derive some quantities from the posterior for statistical inference, for example
    • posterior mean, variance, quantiles, and
    • posterior predictive distribution.
  • We have seen that in many cases, the posterior is only available upto a normalizing constant.
  • There are three types of methods:
    • numerical integration,
    • distributional approximations, and
    • sampling-based methods (Monte Carlo methods).

Monte Carlo Methods

  • Suppose we need to compute \(\E(h(\theta) \mid x)\).

  • The Monte Carlo approximation is \[ \E(h(\theta) \mid x) \approx \frac{1}{m}\sum_{i=1}^m h(\theta^{(i)}), \] where \(\theta^{(1)}, \ldots, \theta^{(m)} \iid \pi(\theta \mid x)\).

  • How to generate iid random samples from an arbitrary distribution?

  • How to do it without knowing the normalizing constant?

Discretization

  • Fix a set of grid values \(\theta_1, \ldots, \theta_N\).
  • Compute \(\pi(\theta_1 \mid x), \ldots \pi(\theta_N \mid x)\) and normalize them such that \[ \sum_{i=1}^N \pi(\theta_i \mid x) = 1. \]
  • Generate \(m\) samples from the multinomial distribution with probabilities \(\pi(\theta_1 \mid x), \ldots, \pi(\theta_N \mid x)\).
  • That is, we approximate \(\pi(\theta \mid x)\) on \(\Theta\) with a multinomial distribution on \(\{\theta_1, \ldots, \theta_N\}\).

Rejection sampling

  • Target distribution: \(\pi(\theta \mid x)\) (possibly unnormalized)
  • We need a proposal distribution \(q(\theta)\) such that
    • it is easy to sample from \(q(\theta)\), and
    • the importance ratio \(\pi(\theta \mid x) / q(\theta)\) is bounded, i.e., \[ \frac{\pi(\theta \mid x)}{q(\theta)} \leq M < \infty, \quad \text{for all } \theta \in \Theta. \]
  • Algorithm:
    1. Sample \(\theta \sim q(\theta)\).
    2. With probability \(\frac{\pi(\theta \mid x)}{M q(\theta)}\), accept \(\theta\) as a draw from \(\pi(\theta \mid x)\). If the drawn \(\theta\) is rejected, return to step 1.
    3. Repeat steps 1 and 2 until \(m\) samples are obtained.

Example

Generate random samples from \(\text{Beta}(\alpha, \beta)\), \(\alpha = 3\) and \(\beta = 4\).

  • Proposal distribution: \(\text{Unif}(0, 1)\).
  • \(M = 3\).

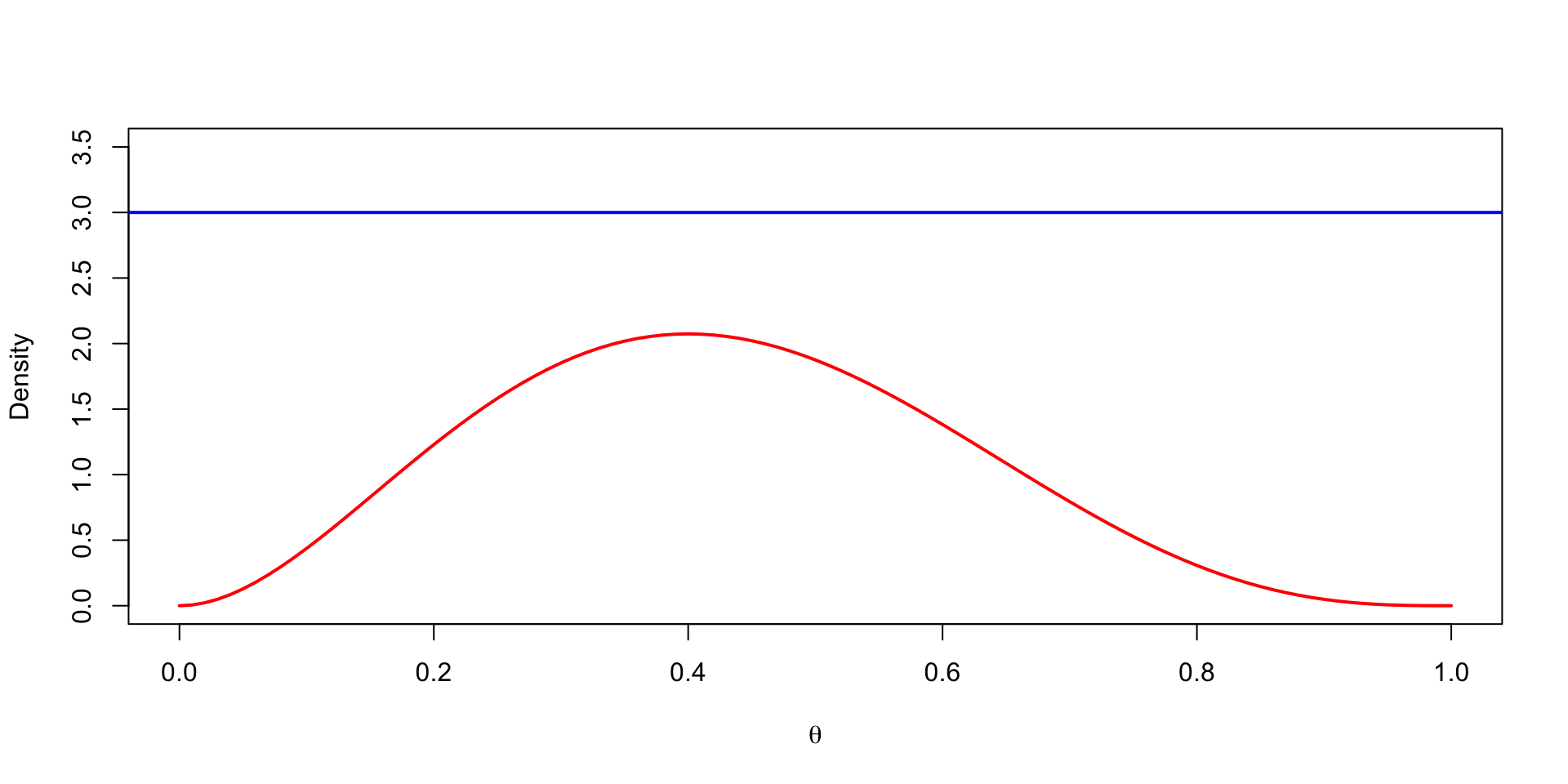
Example

set.seed(2023)
m <- 10000
x <- c()
for(i in 1:m){
    v <- runif(1) # proposal
    
    # rejection step
    u <- runif(1)
    if(u <= dbeta(v, alpha, beta) / (3 * dunif(v))){
        x <- c(x, v)
    }
}

hist(x, freq = FALSE, xlim = c(0,1))
curve(dbeta(x, alpha, beta), col = "red", lwd = 2, add = TRUE)
text(0.1, 2, substitute("accept. rate" == a, 
                        list(a = round(length(x)/m, 2))))

Example

Problems with rejection sampling

  • If \(M\) is large, then the acceptance rate is low, and hence the algorithm is inefficient.
  • You have to know \(\pi(\theta \mid x)\) well to find a good proposal distribution, with a reasonable \(M\).
  • For multivariate distributions, it is virtually impossible to find a good proposal distribution.
  • However, it can be used for simple univariate distributions or truncated distributions.
  • Although rejection sampling produces iid samples from the target distribution, it is inefficient.

Markov Chain Monte Carlo

Markov Chain Monte Carlo (MCMC)

  • MCMC uses samples from a Markov chain whose stationary distribution is the target distribution.
  • Hence the samples are not independent and not from the target distribution.
  • They are only iid from the target distribution asymptotically.
  • The problem is now how to construct a Markov chain whose stationary distribution is the posterior.
  • We will introduce three algorithms:
    • Gibbs sampler
    • Metropolis-Hastings algorithm
    • Hamiltonian Monte Carlo (HMC)

Gibbs Sampler

  • Consider a parameter vector \(\theta = (\theta_1, \theta_2, \ldots, \theta_p)\) with posterior \(\pi(\theta|y)\).
  • If we can sample from the full conditional distributions \(\pi(\theta_i|\theta_{-i}, y)\), then we can construct a Markov chain whose stationary distribution is the posterior.
  • Algorithm:
    • Initialize \(\theta^{(0)} = (\theta_1^{(0)}, \theta_2^{(0)}, \ldots, \theta_p^{(0)})\).
    • For \(t = 1, 2, \ldots, T\):
      1. Sample \(\theta_1^{(t)} \sim \pi(\theta_1|\theta_2^{(t-1)}, \theta_3^{(t-1)}, \ldots, \theta_p^{(t-1)}, y)\).
      2. Sample \(\theta_j^{(t)} \sim \pi(\theta_2|\theta_1^{(t)}, \ldots, \theta_{j-1}^{(t)}, \theta_{j+1}^{(t-1)}, \ldots, \theta_p^{(t-1)}, y)\).
    • Return \(\theta^{(1)}, \theta^{(2)}, \ldots, \theta^{(T)}\).

Example: Bivariate Normal

  • Suppose we want to generate samples from a bivariate normal with mean \(\mu = (\mu_1, \mu_2)\) and covariance matrix \(\Sigma\).
  • Let \([X_1, X_2]^T \sim N(\mu, \Sigma)\). The full conditionals are:
    • \(X_1|X_2 \sim N(\mu_1 + \Sigma_{12}\Sigma_{22}^{-1}(X_2 - \mu_2), \Sigma_{11} - \Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})\).
    • \(X_2|X_1 \sim N(\mu_2 + \Sigma_{21}\Sigma_{11}^{-1}(X_1 - \mu_1), \Sigma_{22} - \Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12})\).
# initialize
mu <- c(0, 0)
Sigma <- matrix(c(1, 0.5, 0.5, 1), nrow = 2)
X <- matrix(0, nrow = 2, ncol = 1000)

# Gibbs sampler
for (t in 2:1000) {
    X[1, t] <- rnorm(1, mu[1] + Sigma[1, 2] / Sigma[2, 2] * (X[2, t-1] - mu[2]), 
                     sqrt(Sigma[1, 1] - Sigma[1, 2] / Sigma[2, 2] * Sigma[2, 1]))
    X[2, t] <- rnorm(1, mu[2] + Sigma[2, 1] / Sigma[1, 1] * (X[1, t] - mu[1]), 
                     sqrt(Sigma[2, 2] - Sigma[2, 1] / Sigma[1, 1] * Sigma[1, 2]))
}

Checking Convergence

# trace plot
par(mfrow = c(1,2))
plot(X[1, ], type = "l", ylab = expression(X[1]), xlab = "Iteration")
plot(X[2, ], type = "l", ylab = expression(X[2]), xlab = "Iteration")

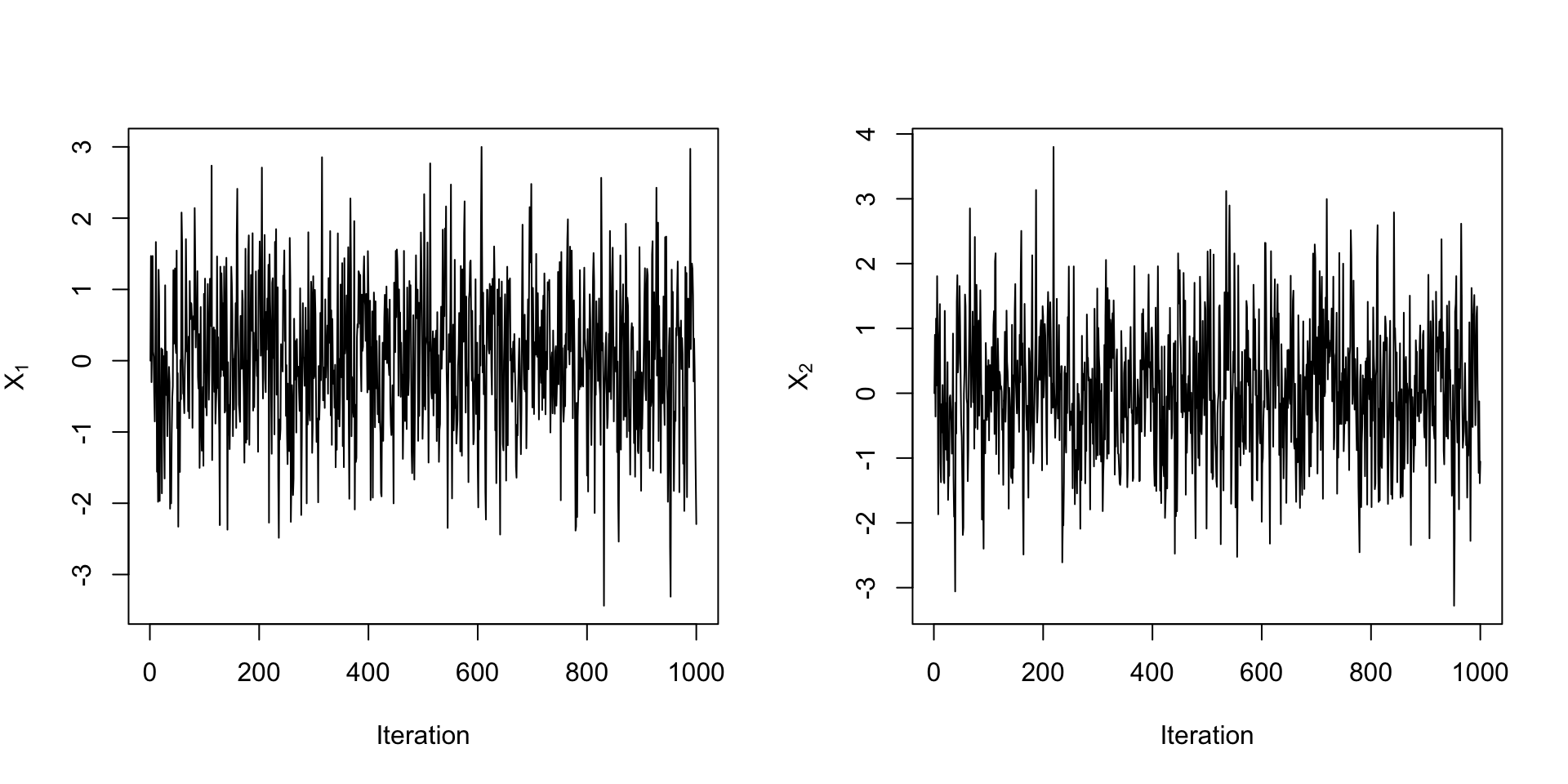
Checking Convergence

X %<>% t() %>% as.data.frame() %>% rename(X1 = V1, X2 = V2) 

ggplot(X, aes(x = X1, y = X2)) + 
    geom_point() + 
    geom_density_2d() + 
    coord_fixed(ratio = 1) + 
    labs(title = TeX("Joint distribution of $X_1$ and $X_2$"))

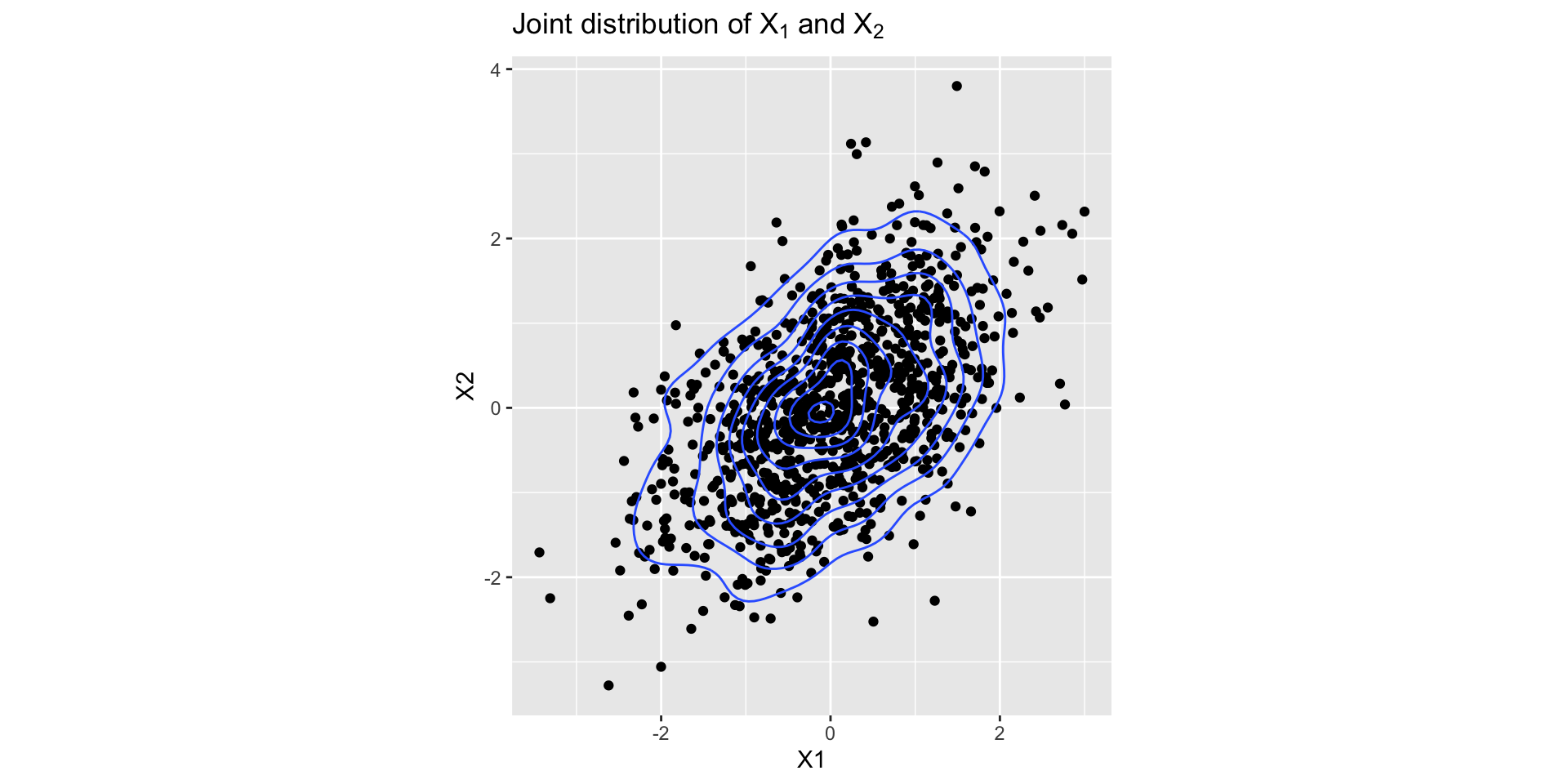
When to use Gibbs sampler?

  • It is useful for multidimensional distributions, especially when the full conditionals are easy to sample from.
  • Even if the full conditionals are not easy to sample from, we can use other algorithms to sample from the conditionals.

Metropolis Algorithm

  • Target distribution: \(\pi(\theta \mid x)\).
  • Proposal distribution at \(t\)th iteration: \(J_t(\theta^* \mid \theta^{(t-1)})\)
    • \(J_t\) needs to be symmetric, i.e., \(J_t(\theta_1 \mid \theta_2) = J_t(\theta_2\mid\theta_1)\).
  • Algorithm:
    1. At \(t\)th iteration, sample \(\theta^*\) from \(J_t(\theta^* \mid \theta^{(t-1)})\).
    2. Compute the acceptance ratio \(\rho(\theta^{(t-1)}, \theta^{*})=\min\left\{\frac{\pi(\theta^* \mid x)}{\pi(\theta^{(t-1)} \mid x)}, 1\right\}\).
    3. Set \[ \theta^{(t)}= \begin{cases}\theta^* & \text { with prob. } \rho(\theta^{t-1}, \theta^{*}) \\ \theta^{(t-1)} & \text { with prob. } 1-\rho(\theta^{(t-1)}, \theta^{*}).\end{cases} \]
  • Intuition: if \(\theta^*\) is more likely than \(\theta^{(t-1)}\), then accept \(\theta^*\); otherwise, accept \(\theta^*\) with probability \(\rho(\theta^{(t-1)}, \theta^{*})\).

Example

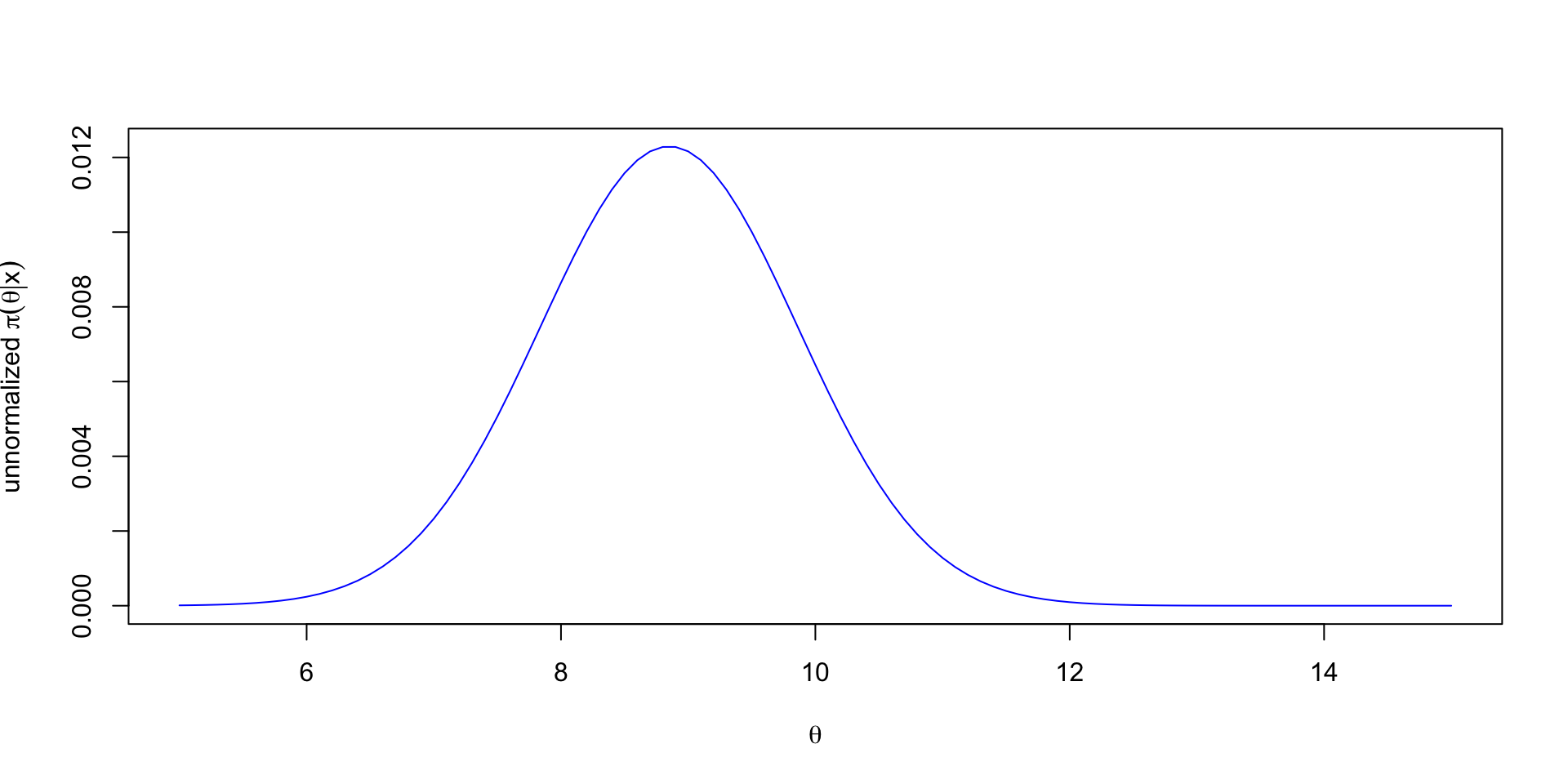
  • Suppose \(X \mid \theta \sim N(\theta, 1)\) and \(\theta \sim \text{Cauchy}(0, 1)\).
  • The posterior is \(\pi(\theta \mid x) \propto \frac{1}{1+\theta^2}\exp\left(-\frac{1}{2}(x-\theta)^2\right)\).
  • A commonly used proposal is \(J_t(\cdot \mid\theta^{(t-1)}) = N(\theta^{(t-1)}, \sigma^2)\), where \(\sigma^2\) is a tuning parameter.
# generate sample
set.seed(2023)
theta_0 <- rcauchy(1, 0, 1)
X <- rnorm(1, theta_0, 1)

# log posterior
log_post <- function(theta, x) {
    -log(1 + theta^2) - 0.5 * (x - theta)^2
}
curve(exp(log_post(x, X)), 5, 15, 
      ylab = TeX("unnormalized $\\pi(\\theta | x)$"), 
      xlab = TeX("$\\theta$"), col = "blue")

Example

Example

# Metropolis algorithm
T <- 1000
theta <- rep(0, T)
theta[1] <- rnorm(1, 0, 1)
accept <- 0
for (t in 2:T) {
    theta_star <- rnorm(1, theta[t-1], 1)
    r <- exp(log_post(theta_star, X) - log_post(theta[t-1], X))
    theta[t] <- ifelse(runif(1) < r, 
                       {accept <- accept + 1; theta_star},
                       theta[t-1])
}
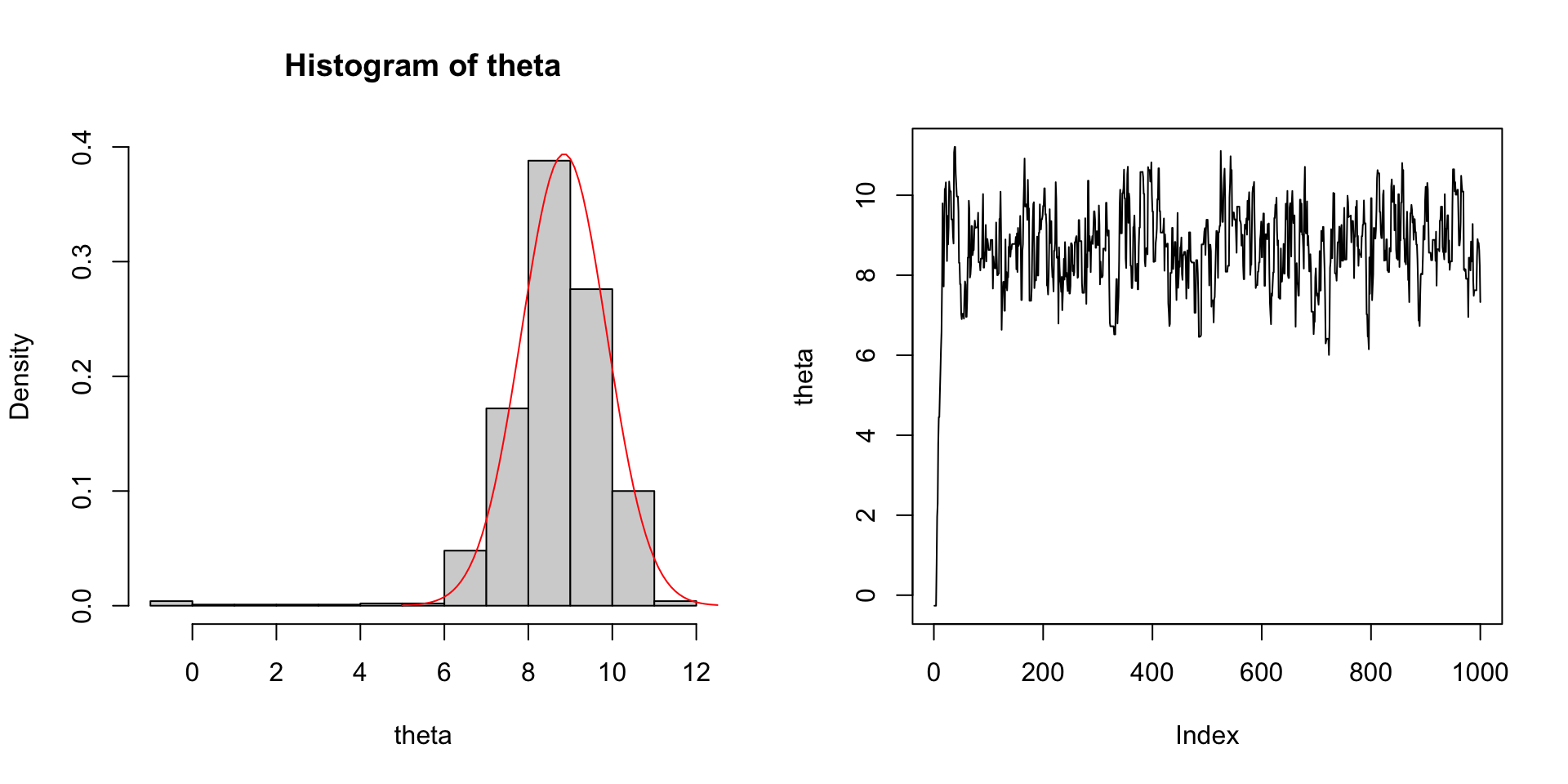
  • Acceptance rate: 0.702.
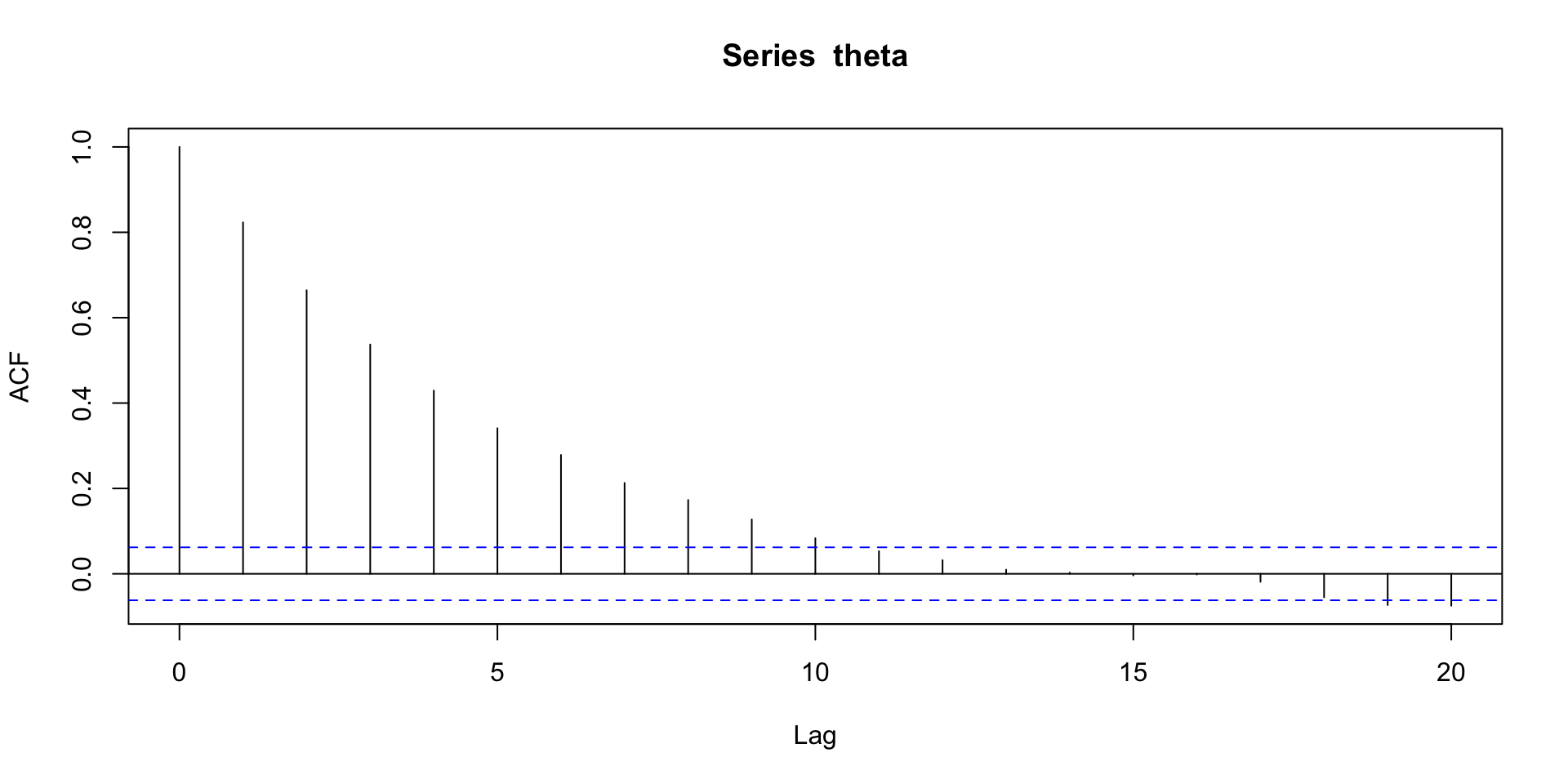
  • Autocorrelation (lag 1): 0.823, i.e., the correlation between \(\theta^{(t-1)}\) and \(\theta^{(t)}\).
  • Posterior mean: 8.635.

Example

# normalizing constant
Z <- integrate(function(theta) exp(log_post(theta, X)), -Inf, Inf)$value

par(mfrow = c(1,2))

hist(theta, freq = FALSE, ylim = c(0, 0.4))
curve(exp(log_post(x, X))/Z, 5, 15, add = TRUE, col = "red")

plot(theta, type = "l")

Advantages of Metropolis Algorithm

  • It can be seen as a improvement of rejection sampling.
  • We don’t need to know the target distribution well to choose a proposal distribution.
  • The trade-off is that the generated samples are not longer iid.
  • We can tune the proposal distribution to improve the acceptance rate making the algorithm more efficient.

Metropolis-Hastings Algorithm

  • Metropolis-Hastings algorithm is a generalization of Metropolis algorithm, in that it does not require symmetric proposals.
  • For a proposal distribution \(J_t(\theta_a \mid \theta_b)\), the unconditional probability from \(\theta_a\) to \(\theta_b\) is \[ p(\theta^{t-1} = \theta_a, \theta^{t} = \theta_b) = J_t(\theta_b \mid \theta_a)\pi(\theta_a \mid x). \]
  • Hence the acceptance ratio becomes \[\begin{align*} \rho(\theta^{t-1}, \theta^{*}) & = \min\left\{\frac{p(\theta^{t-1} = \theta^{t-1}, \theta^{t} = \theta^{*})}{p(\theta^{t-1} = \theta^{*}, \theta^{t} = \theta^{t-1})},1\right\}\\ & = \min\left\{\frac{J_t(\theta^{t-1} \mid \theta^{*})\pi(\theta^{*} \mid x)}{J_t(\theta^{*} \mid \theta^{t-1})\pi(\theta^{t-1} \mid x)},1\right\}. \end{align*}\]
  • This modification allows us to use a wider range of proposal distributions and hence improve the efficiency of the algorithm.

Why it works?

  • It is obvious that MH generates a Markov chain. Why does it converge to the target distribution?
  • Detailed balance condition1: A Markov chain has a stationary distribution \(\pi\) if it satisfies the equation \[ \pi(\theta_a)\P(X_t = \theta_b \mid X_{t-1} = \theta_a) = \pi(\theta_b)\P(X_t = \theta_a \mid X_{t-1} = \theta_b). \]
  • Proof (sketch): \[\begin{align*} & \quad \pi(\theta_a \mid x)\P(X_t = \theta_b \mid X_{t-1} = \theta_a)\\ &= \pi(\theta_a \mid x)J_t(\theta_b \mid \theta_a) \rho(\theta_a, \theta_b) \\ & = \pi(\theta_a \mid x)J_t(\theta_b \mid \theta_a) \min\left\{\frac{J_t(\theta_a \mid \theta_b)\pi(\theta_b \mid x)}{J_t(\theta_b \mid \theta_a)\pi(\theta_a \mid x)},1\right\}\\ & = \min\left\{J_t(\theta_a \mid \theta_b)\pi(\theta_b \mid x), J_t(\theta_b \mid \theta_a)\pi(\theta_a \mid x)\right\} \end{align*}\]

Ergodic Theorems

  • Now we know that the MH algorithm generates a Markov chain \(\theta_1, \theta_2, \ldots\) with a stationary distribution \(\pi(\theta \mid x)\).
  • We need to use these MCMC samples to estimate posterior quantities, for example, \[ \frac{1}{M}\sum_{i=1}^M h(\theta_i). \]
  • If the \(\theta_i\)’s are iid, then we can use the CLT to obtain the consistency and the asymptotic distribution of the above estimator.
  • For Markov chains, we have ergodic theorems, which state that if \(\theta_1,\theta_2,\ldots\) is ergodic, we have the CLT.
  • See Ch. 6 & 7 of Monte Carlo Statistical Methods by Robert & Casella (2004) for details.

Guidelines for choosing proposal distribution

  • For any \(\theta\), it is easy to sample from \(J\left(\theta^* \mid \theta\right)\).
  • It is easy to compute the ratio \(\rho\).
  • Each jump goes a reasonable distance in the parameter space (otherwise the random walk moves too slowly).
  • The jumps are not rejected too frequently (otherwise the random walk wastes too much time standing still).

Combining Gibbs and MH

  • In fact, Gibbs sampler is a special case of MH, with the proposal being the conditional distribution: \[ J_{j, t}^{\text {Gibbs }}\left(\theta^* \mid \theta^{(t-1)}\right)= \begin{cases}\pi\left(\theta_j^* \mid \theta_{-j}^{(t-1)}, x\right) & \text { if } \theta_{-j}^*=\theta_{-j}^{(t-1)} \\ 0 & \text { otherwise. }\end{cases} \]
  • We can use MH to sample from \(\pi\left(\theta_j^* \mid \theta_{-j}^{(t-1)}, x\right)\). This is called Metropolis-within-Gibbs.
  • In cases where some conditionals are easy to sample from but others are not, Metropolis-within-Gibbs will be more efficient than a simple MH.

Diagnostic of MCMC

Diagnostic of MCMC samples

Suppose now we have a sequence of MCMC samples: \(\theta_1, \ldots, \theta_m\).

  • Did I run the chain long enough so that the samples are roughly from the target distribution?
  • How strong is the dependence between the samples?
  • How to fix these problems?

Mixing and convergence

  • Convergence: whether the chain has converged to the target distribution.
  • Mixing: Multiple chains should mix together.

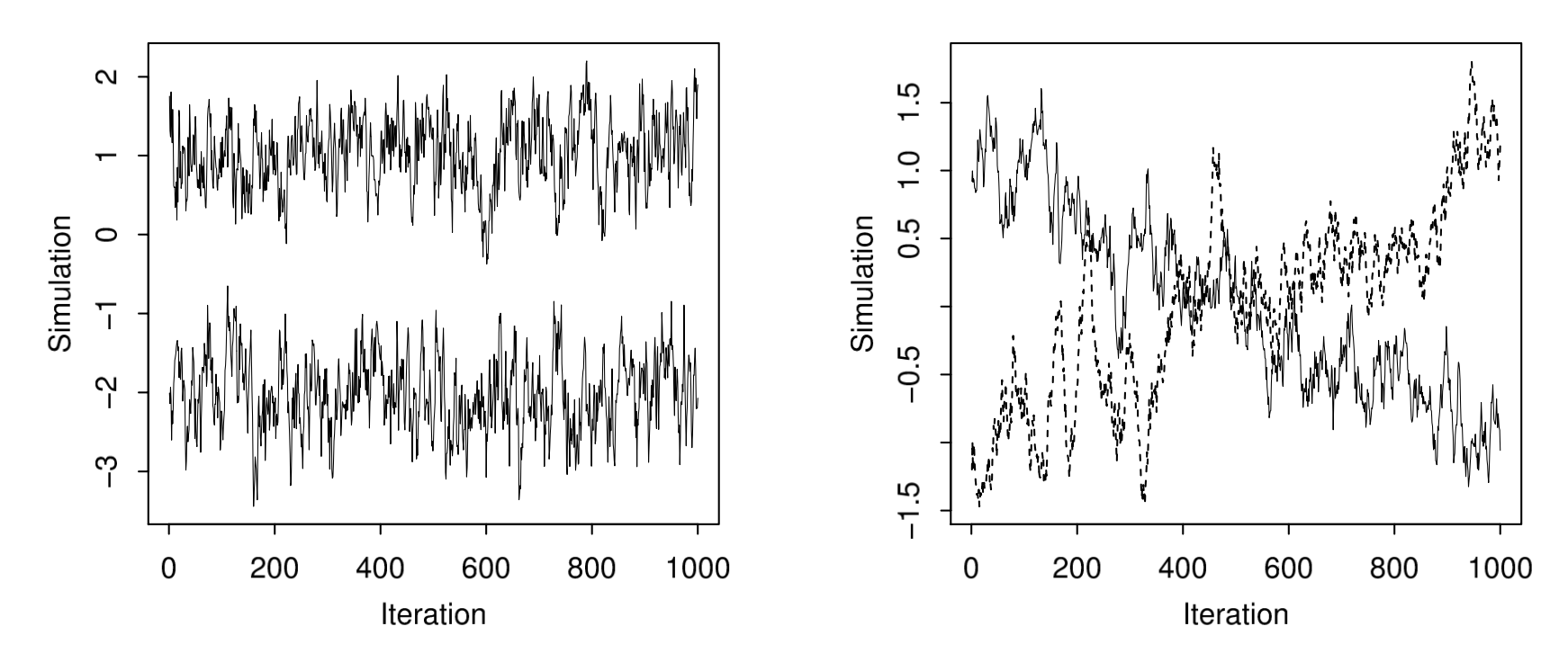
Fig 11.3 of BDA

Autocorrelation

Lag-\(k\) Autocorrelation: the correlation between \(\theta^{(t)}\) and \(\theta^{(t+k)}\) for \(k > 0\).

acf(theta, lag.max = 20)

Effective sample size

  • We can compute an approximate ``effective number of independent simulation draws’’ for any estimand of interest \(\psi\).
  • The effective sample size is defined as \[ \text{ESS} = \frac{m}{1 + 2\sum_{k=1}^\infty \rho_k}, \] where \(m\) is the length of a chain and \(\rho_k\) is the lag-\(k\) autocorrelation.
  • Different estimates of \(\rho_k\)’s give different ESS’s.
library(coda)
library(mcmcse)

print(paste("ESS:", round(coda::effectiveSize(theta), 2)))
[1] "ESS: 96.85"
print(paste("ESS:", round(mcmcse::ess(theta), 2)))
[1] "ESS: 113.83"

Practical tricks

  • Burn-in: discard the first few samples.
  • Thinning: keep only every \(k\)-th sample.
  • Simulated annealing: start with a large variance (of proposal) and gradually reduce it.
  • Parallel tempering: run multiple chains with different temperatures and swap chains occasionally: for \(1 < T_1 < T_2 < \cdots < T_n\), the \(i\)-th chain has target distribution \[ \pi_i(\theta) \propto \pi(\theta)^{1/T_i} = \exp\left\{\frac{1}{T_i}\log\pi(\theta)\right\}. \]
  • Data augmentation: introduce latent variables to make the target distribution more tractable, i.e., find \(\nu\) such that \[ \pi(\theta \mid x) = \int \pi(\theta \mid \xi, x) \nu(\xi)d\xi. \]

Example

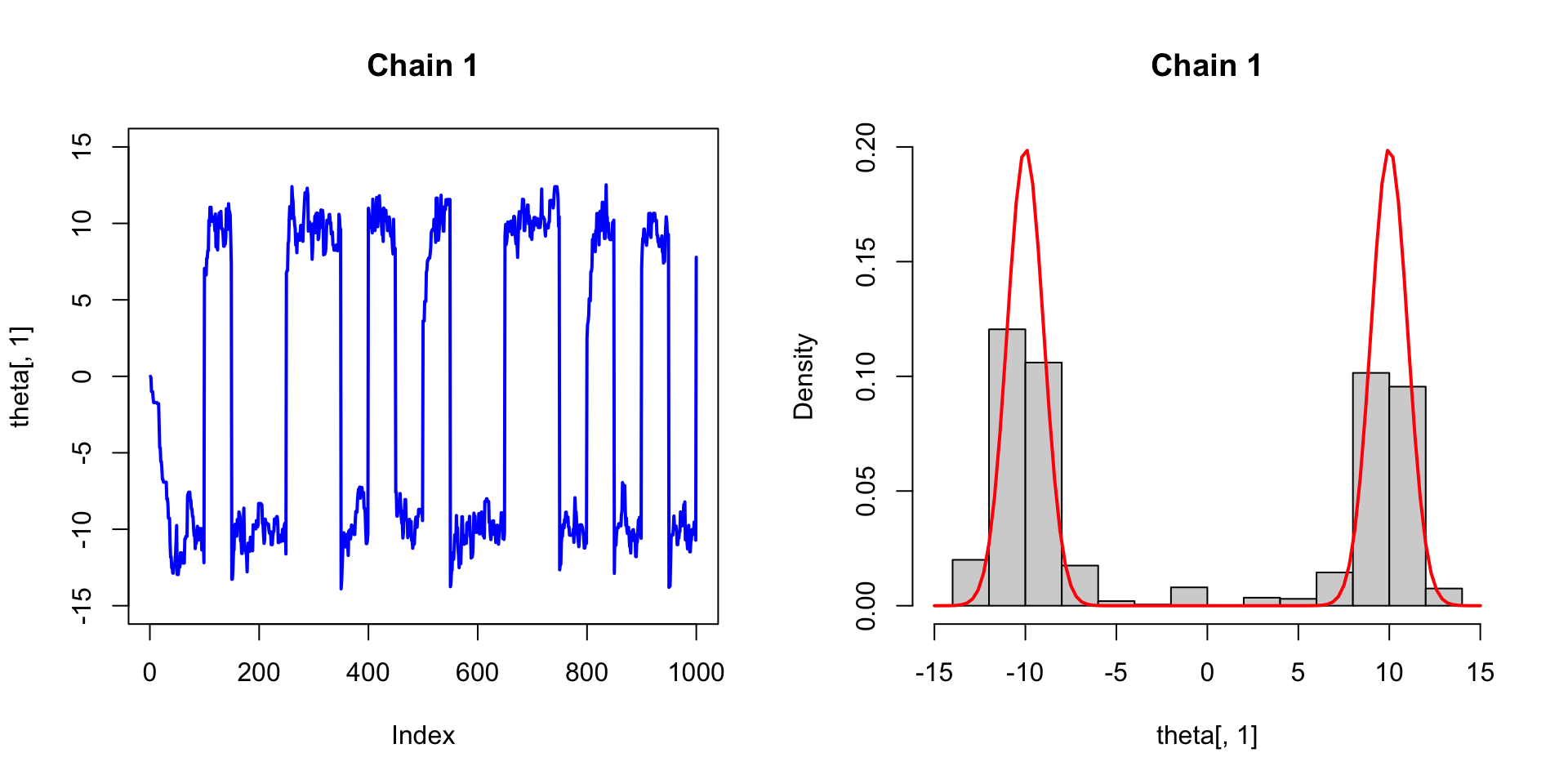
Suppose the target distribution is \(\pi(\theta) = \frac{1}{2}N(10,1) + \frac{1}{2}N(-10, 1)\).

log_post <- function(x){
    log(dnorm(x, 10, 1)/2 + dnorm(x, -10, 1)/2)
}
curve(exp(log_post(x)), -15, 15, col = "red", lwd = 2)

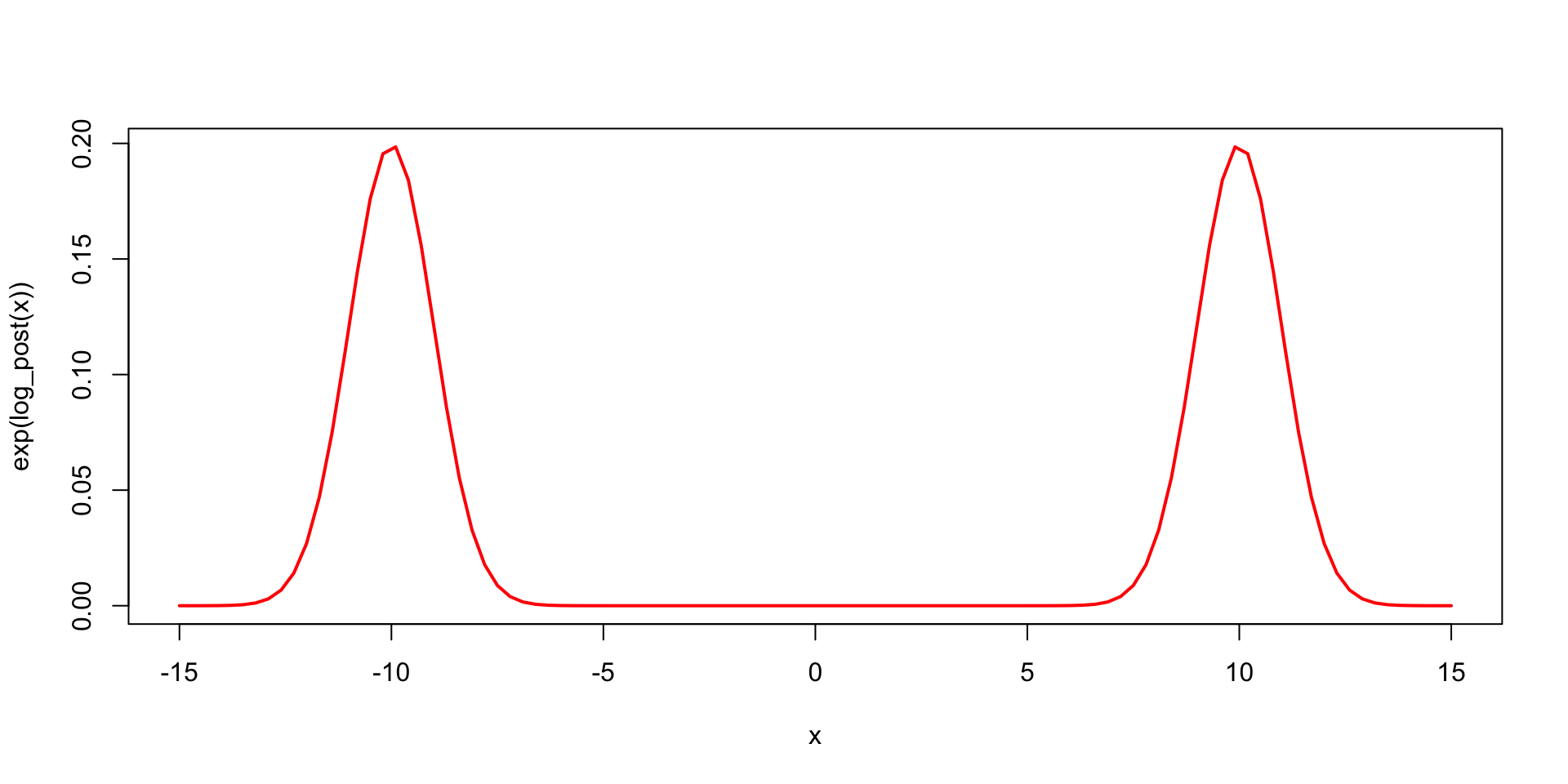
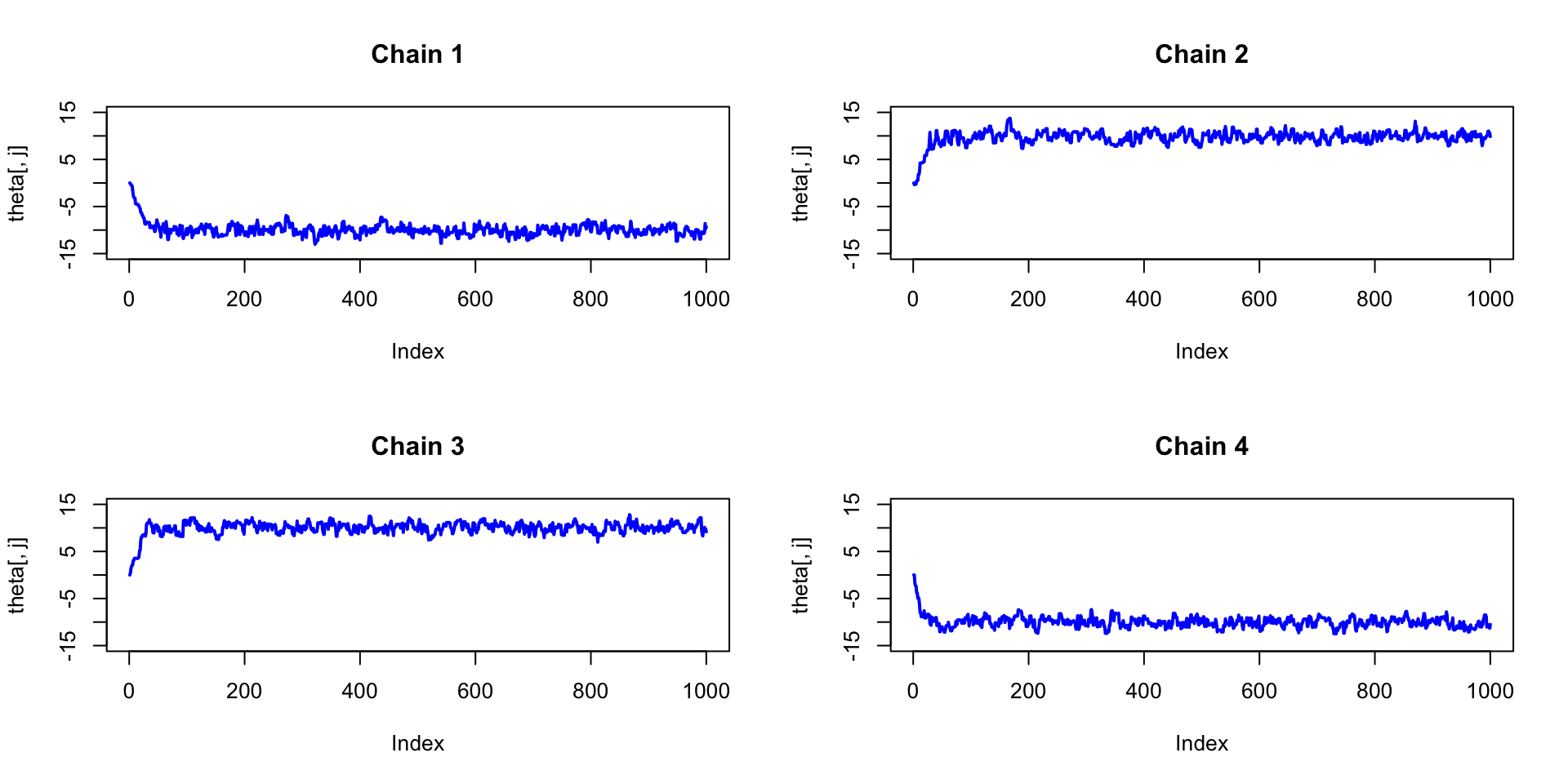
Vanilla Metropolis

set.seed(2023)
M <- 1000; n_chain <- 4
theta <- matrix(0, ncol = 4, nrow = M)

for (j in 1:n_chain){
    for (i in 2:M){
        theta.star <- rnorm(1, theta[i-1,j], 1)
        rho <- exp(log_post(theta.star) - log_post(theta[i-1,j]))
        if (runif(1) < rho){
            theta[i,j] <- theta.star
        } else {
            theta[i,j] <- theta[i-1,j]
        }
    }
}

Vanilla Metropolis

par(mfrow = c(2,2))
for (j in 1:n_chain){
    plot(theta[,j], type = "l", col = "blue", lwd = 2, 
         ylim = c(-15, 15), main = paste("Chain", j))
}

Parallel tempering

set.seed(2023)
M <- 1000; n_chain <- 4
theta <- matrix(0, ncol = 4, nrow = M)
temp <- c(1, 10, 20, 40); swap_int <- 50

for (i in 2:M){
    for (j in 1:n_chain){
        theta.star <- rnorm(1, theta[i-1,j], 1)
        rho <- exp(log_post(theta.star)/temp[j] -
                       log_post(theta[i-1,j])/temp[j])
        if (runif(1) < rho){
            theta[i,j] <- theta.star
        } else {
            theta[i,j] <- theta[i-1,j]
        }
    }
    # Swap chains
    if(i %% swap_int == 0){
        for (j in 1:(n_chain-1)){
            rho <- exp(log_post(theta[i,j])/temp[j+1] +
                           log_post(theta[i,j+1])/temp[j] - 
                           log_post(theta[i,j])/temp[j]-
                           log_post(theta[i,j+1])/temp[j+1])
            if (runif(1) < rho){
                theta[i,] <- theta[i, c(j+1, j)]
            }
        }
    }
}

Parallel tempering

par(mfrow = c(1,2))
plot(theta[,1], type = "l", col = "blue", lwd = 2, 
         ylim = c(-15, 15), main = paste("Chain", 1))
hist(theta[,1], freq = F, xlim = c(-15, 15), 
     ylim = c(0, 0.2), main = "Chain 1")
curve(exp(log_post(x)), -15, 15, col = "red", lwd = 2, add = TRUE)

Home